Rotate Array

    

 Leetcode - 189

Rotate Array

Problem: https://leetcode.com/problems/rotate-array/

The given problem expects the given array to be rotated to the right by k steps. 

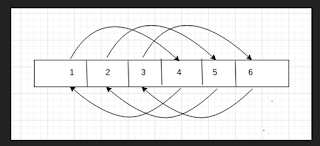
For example, given [1, 2, 3, 4, 5, 6] and k = 3, we need to perform the following:

and hence we get the array, [4, 5, 6, 1, 2, 3]

We can generalize the problem as following:

Given an array of n-elements, perform m-rotations by magnitudes r[0], r[1], ...., r[m-1] given as array r, either by left or right given by array d[0], d[1], d[2], ...., d[m-1]. If d[i] = 0, then rotate left or rotate right otherwise.

We try solving this version of the problem. Finally we reduce the generalized problem into the original problem.

Solution 1: Bruteforce -  O(mn) time, O(1) space

We try solving the problem by following word by word as described in the problem statement. We need to rotate every a[i] by r[i] positions to the left if d[i] = 0 or to the right otherwise. 

We can use modular arithematic and rotate by the magnitude of r[i]%n instead of r[i], since r[i] can also be greater than n. If we rotate by n-positions, it is same as not rotating at all. And hence we can rotate by r[i]%n to make sure rotation magnitude is between 0 and n-1(inclusive). 

    void rotations(vector<int>& a, vector<int>& r, vector<int>& d) {
	int m = r.size();
	for(int i = 0; i<m; ++i)
	    if(d[i] == 0) {
                rotate_right(a, n, r[i]%n);
	    } else {
		rotate_left(a, n, r[i]%n);
	    }
	}
    }       
 

We can notice that time complexity of the code is dependent on how efficiently we implement rotate_left and rotate_right functions. Time complexity of rotate = O(m* time complexity of rotate left or right).

Let us try deducing a method to perform rotation of an array to the right by r positions.

Solution 1a: MOVE ONE ELEMENT AT A TIME - O(nr) time, O(1) time  

One way is to rotate one position and repeat for r-times. We need to store nth element into a temporary variable as the (n-1)th element will overwrite it.

     void rotate_right(vector<int>& a, int r) {
 	        while(r--) {
 		    rotate_right_by_one_pos(a);
 	        }
         }

     void rotate_right_by_one_pos(vector<int>& a) {
 	    int temp = a[a.size() - 1];
 	    for(int j = a.size() - 2; j>=0; j--) {
      	    a[j+1] = a[j];
              }
            a[0] = temp;
       }
 

This method will make rotate_right(), O(nr) time complexity i.e quadratic and hence rotate() cubic. No extra space is needed.

Solution1b: MOVE A BLOCK OF ELEMENTS - O(n) time, O(n) space

The idea is to allocate an auxiliary biffer of r-elements and use it as temporary storage to store rightmost r-elements. Displace the first (n-r) elements to the left and copy the elements in the temp storage to the beginning of the modified array a.

    void rotate_right(vector<int>& a, int r) {
        vector<int> temp(r, -1);
        for(int i = a.size() - 1 - r, j = 0; j<r; ++i, ++j) {
            temp[j] = a[i];
        }
        for(int i = a.size() - 1 - r; i>=0; --i) {
            a[i+r] = a[i];
        }
        for(int i = 0; i<r; ++i) {
            a[i] = temp[i];
        }
    }

Although this method takes just linear time to rotate_right and hence quadratic time to rotate(), we use a O(n) extra space.

Solution 1c: MOVE EACH ELEMENT TO ITS TARGET POSITION: (Cyclic Permutation) - O(n) time, O(1) space

The idea is to move each element r-positions to the right (modulo n) i.e a[i] goes to a[(i+r)%n]. We try processing elements as a cycle of elements which contains a[i], a[(i+r)%n], a[(i+2r)%n], ..., a[i]. Once an element belongs to a cycle and is processed, it doesn't belong to any other cycle and hence we can ensure a O(n) time complexity. Processing an element implies displacing an element to a next position i.e (i+r)%n the position in the cycle formed. 

Consider the example of [1, 2, 3, 4, 5, 6] and k = 2.

The important question to be answered is how many cycles are formed in an array of length n with each element at a distance of r?

Let us assume that we start at index i. The element a[i] moves to index (i+r)%n, and the element at its position moves to (i+2r)%n position and so on..

Let the length of the cycle formed = k, Therefore, (i+kr)%n = i as it is a cycle. And hence, kr should be a multiple of n i.e n | kr or n divides kr as (i+kr)%n = i.

Now we have the facts that n | kr and also obviously r | kr and k is smallest such value i.e the length of our cycle is the smallest possible.

Now from general arithematic, LCM(a, b) * GCD(a, b) = a * b, for all a, b being integers.

Therefore,

kr = LCM(n, r) => kr = nr / GCD(n, r) => k = n / GCD(n, r)

    void rotate_right(vector<int >& a, int r) {
        for(int start = 0; start < gcd(n, r); ++i) {
            int next_inx = start;
            int ele = a[start];
            do {
                next_inx = (next_inx + r) % n;
                int temp = a[next_inx];
                a[next_inx] = ele;
                ele = temp;
            } while(next_inx != start) ;
        }
    }
  
 

Therefore, the length of each cycle is [n / GCD(n, r)] and hence we will have GCD(n, r) number of cycles.

Hence, for every cycle, we process each element and displace it to its next position in the cycle.

Time complexity of this algorithm is O(n) as each element is moved exactly once and assuming GCD(x, y) takes less that or equals to O(n). No extra space used!

NOTE: GCD(a, b) can be computed using Euclid's method which has a theoritical bound of O(logb) where   a >= b.

It states, GCD(a, b) = GCD(b, a%b) and GCD(a, 0) = a.

Solution1d: MULTIPLE REVERSES - O(n) time, O(1) space:

Let array a = xy where x = a[0], a[1], ..., a[n-r-1] and y = a[n-r], a[n-r+1], .. a[n-1].

The aim is to get a = yx from a = xy. Let x^r represent reverse of x.

Step 1: Reverse a => 

a = xy becomes a = (xy)^r =  y^rx^r

Step 2: Reverse first r-elements => 

a =  y^rx^r becomes a = (y^r)^rx^r = yx^r

Step 3: Reverse the rightmost (n-r) elements

a =  yx^r becomes a = y(x^r)^r  = yx which is the target

    void rotate_right(vector<int>& a, int r) {
        reverse(nums.begin(), nums.end());
        reverse(nums.begin(), nums.begin() + k);
        reverse(nums.begin() + k, nums.end());
    }
    

We use no extra space and time complexity is O(n) + O(n-r) + O(r) = O(n) and hence linear making rotate() quadratic.

Solution 2: Using Effective Rotation magnitude -  O(n) time, O(1) space:

Unitl now, the best performance we have achieved is by a quadratic time algorithm and constant space algorithm. This is because we repeat the rotation for every m-elements. Instead of this we can calculate rotation magnitude and then rotate by that amount. Also instead have 2 directions left and right to rotate, we can consider left rotation as a negative form of right direction and subtract from effective rotation magnitude.

    void rotations(vector<int>& a, vector<int>& r, vector<int>& d) {
	int m = r.size(), n = a.size();
        int eff = 0;
	for(int i = 0; i<m; ++i)
	    if(d[i] == 0) {
                eff = (eff - r[i])%n;
	    } else {
		eff = (eff + r[i])%n;
	    }
	}   
        if(eff < 0) eff = eff + n;
        rotate_right(a, eff);
    }     

Now we can see that m-rotation can be done in O(n) time complexity and O(1) extra space.

And the solution to the original leetcode question, is the function rotate_right() discussed above which can be done in O(n) time and O(1) time.