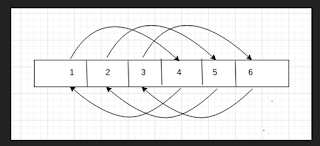
2. Contains Duplicate - II
For example, given an array [1, 2, 2, 1] and k = 2, for every index
check if an duplicate exists at or within 2 elements next to index
and at or within 2 elements before the index. The following
subarrays are obtained: [1, 2, 2], [1, 2], [2, 2, 1], [1, 2, 2], [2,
1], [2, 2, 1]. We have subarrays with duplicate values and
hence, the answer is True.
Solution 1: Brute-Force method - O(nk) time ,O(n) space [TLE]
A typical solution would be to follow the problem description
i.e. create subarrays of size <= k+1 for every index and
checking for duplicates in these subarrays.
For checking duplicates in a k+1 elements window/subarray, we
have an empty unordered set(as it uses a hash table which provides
constant time basic operation) which is cleared after every index
is processed. As we process a new element, if it already exists in
the set, then it indicates a presence of a duplicate. If all
indexes are processed successfully, then we have failed to find
desired subarrays with duplicates.
bool bruteforce(vector<int>& nums, int k) {
int n = nums.size();
unordered_set<int> set;
for(int j = 0; j <=k && j < n; ++j) {
if(set.count(nums[j]) == 1) {
return true;
}
set.insert(nums[j]);
}
for(int i = 1; i+k<n; ++i) { // O(n) times
set.clear();
for(int j = 0; j <= k; ++j) { // O(k) times for each i
if(set.count(nums[i+j]) == 1) {
return true;
}
set.insert(nums[i+j]); // O(1) time for one call
}
}
return false;
}
Complexity analysis:
To process every index we need to check for duplicates in a k+1 sized
subarray starting from 0 sized subarray/window which takes O(k) time
and this process needs to be repeated for every element in the array
which effectively gives an time complexity of O(nk) or
O(n2) as k<=n for the whole algorithm. It also consumes
O(k) or O(n) as k<=n space for an unordered set.
Solution 2: Using
Balanced BST - O(n logk) time, O(k) extra space
The Brute Force solution hurts because for every index to be
processed it starts processing from zero sized window and progresses
to a k+1 sized window. This can improved by using a constant sized
sliding winow approach of size k+1. This helps as the approach uses
information from previous state of the window and makes only minimum
changes as much as needed to create a new window.
In this solution, we use a set which uses a balanced BST for
internal implemenation. Initialize a window of size k+1 from
beginning of the array and also insert them into the set. Then slide
the winow by one element to the right. As k elements in the new
window will be same as previous state of the window, we do not clear
the set as in brute force, rather we just remove the element from
the set which slid out of the window and insert new element that
slid in into the window.
In the process, if an element to be inserted already exists, then
it indicates a duplicate.
bool orderedset(vector<int>& nums, int k) {
int n = nums.size();
set<int> set;
// initialize the window
for(int j = 0; j <=k && j < n; ++j) {
if(set.count(nums[j]) == 1) {
return true;
}
set.insert(nums[j]);
}
for(int i = 1; i+k<n; ++i) { // O(n) times
set.erase(nums[i-1]);
if(set.count(nums[i+k]) == 1) {
return true;
}
set.insert(nums[i+k]);
}
return false;
}
Complexity analysis:
We use a balanced BST which taken O(logn) for basic operations and
insertion and deletion has to be done for n-k+1 windows. Hence the
time complexity of the algorithm is O(nlogn) as k<=n. As we use a
balanced BST, it constributes as an extra space of O(n) as
k<=n.
Solution 3: Using Hash
Table - O(n) time, O(k) extra space
Solution 2 can be made efficient by using choosing a more efficient
data structure for the purpose. We can use a Hash Table(Unordered
Sets) instead of a balanced BST(Set) as in a Hash Table, basic
operations take constant time.
Rest all implementation details and algorithm of solution 3 is same
as in solution 2 discussed above.
bool lineartime(vector<int>& nums, int k) {
int n = nums.size();
unordered_set<int> set;
for(int j = 0; j <=k && j < n; ++j) {
if(set.count(nums[j]) == 1) {
return true;
}
set.insert(nums[j]);
}
for(int i = 1; i+k<n; ++i) { // O(n) times
set.erase(nums[i-1]);
if(set.count(nums[i+k]) == 1) {
return true;
}
set.insert(nums[i+k]);
}
return false;
}
Complexity analysis:
Space complexity is same as solution 2 which is linear. Use of Hash
Table based data structure makes insert and erase work in constant
time and hence for n-k+1 windows, the overall time complexity will
effectively be on a average O(n) as k<=n when compared to O(nlogn)
of previous solution.
3. Contains Duplicate - III
The given problem is same as Contains Duplicate-II, but with an
extra constraint that the window [i, j] should also satisfy the
condition that abs(nums[i] - nums[j]) <= t. In the example
discussed for the above problem, we had got [1, 2, 2], [1, 2], [2, 2, 1], [1, 2, 2], [2, 1], [2, 2, 1] and
for t = 2, the array also satisfies the desired constraints for
the current problem as in the 1st subarray itself we have (2-1 =
1) <= (t = 2).
Solution 1: Using Ordered Set - O(nlogk) time and O(k) extra
space
The solution to this problem will have all the concepts from
Contains Duplicate-II solution using a set/balanced BST and some
extra concepts. We use lower_bound function which is efficient in a
balanced BST rather than a Hash Table to check if an
element is in the range nums[i+k]-t to nums[i+k]+t for every
nums[i].
To cover both index range and value range validity in one
condition, we check if the lower bound of nums[i+k] - t and lower
bound of nums[i+k]+t+1 which is outside the desired range num[i+k]-t
and nums[i+k]+t are not equal. If the iterators returned by the mentioned lower bound calls are not equal, then we have found a subarray which matches the description of the problem and hence return true. On sliding
the window, we remove the element at the tail of the set and add the
new element that slid in as usual.
NOTE: We need to take care the overflow of nums[i+k]+t+1 and underflow of nums[i+k]-t. So if nums[i+k]+t+1 > INT_MAX, then set it to INT_MAX and if nums[i+k]-t < INT_MIN, then set it to INT_MIN.
bool orderedset(vector<int>& nums, int k, int t) {
int n = nums.size();
set<int> set;
for(int j = 0; j <=k && j < n; ++j) {
int lb = (nums[j] <= INT_MIN + t) ? INT_MIN : (nums[j] - t);
int ub = (nums[j] >= INT_MAX - t - 1) ? INT_MAX : (nums[j] + t + 1);
if(set.lower_bound(lb) != set.lower_bound(ub)) { // O(log k) time
return true;
}
set.insert(nums[j]);
}
for(int i = 1; i+k<n; ++i) { // O(n) times
set.erase(nums[i-1]);
// see if any entry is in the range nums[i+k]-t to nums[i+k]+t
int lb = (nums[i+k] <= INT_MIN + t) ? INT_MIN : (nums[i+k] - t);
int ub = (nums[i+k] >= INT_MAX - t - 1) ? INT_MAX : (nums[i+k] + t + 1);
if(set.lower_bound(lb) != set.lower_bound(ub)) { // O(log k) time
return true;
}
set.insert(nums[i+k]);
}
return false;
}
NOTE:
set_name.lower_bound(key); returns the iterator to the key in the set. If key is not present, then it returns an iterator pointing to the immediate next element which is greater than k. In simple words, it returns a iterator to a value whose magnitude is "atleast key"(value >= key) in the container which is exactly one of the constraint in the problem.
Complexity analysis:
Finding lower_bound on a balanced BST is analogous to search which
takes O(logk). Hence finding lower found for n-k+1 windows will
effectively give a time complexity of O(nlogn) as k<=n. Use of
set data structures takes O(k) or O(n) extra space.
Comments
Post a Comment