MEDIAN FROM DATA STREAM
Leetcode - 295
Find Median From Data Stream
For a given stream of integers we need to return the median. Median is the middle value in a sorted integer list with odd number of elements and if the list has even number of elements then median is mean of two middle values.
Solution 1: Brute-force - O(nlogn), O(1) time, O(1) space [TLE]
In this method we follow the most trivial method to find the median. We sort the container which stores the input from the stream. From the sorted container find the middle value(s) to find the median. The container can a vector as we can sort it easily, insert at the end in constant time and elements are indexed to find the middle value(s).
vector<int> arr; MedianFinder() { } void addNum(int num) { arr.push_back(num); sort(arr.begin(),arr.end()); } double findMedian() { if(arr.size()%2==1) return arr[arr.size()/2]; else return (arr[arr.size()/2]+arr[arr.size()/2 -1])/2.0; }
Complexity analysis:
Sorting takes O(nlogn) and finding the median takes O(1) time. Hence the time complexity of addNum() becomes O(nlogn) and findMedian() is O(1). We do not use any extra space other than the container to store the stream of inputs.
Solution 2: Insertion sort method - O(n), O(1) time, O(1) space [TLE]
Instead of sorting after inserting the new element, we insert the new element to the position where it's supposed be in a sorted container. This method is analogous to the concept of insertion sort. This method still ensures that the container is sorted at all times. And hence median is still the middle value(s) of the list.
Complexity analysis:
The time complexity of addNum() will reduce to O(n) from O(nlogn) of previous solution and findMedian() still works in constant time and the whole solution still doesn't use any extra space.
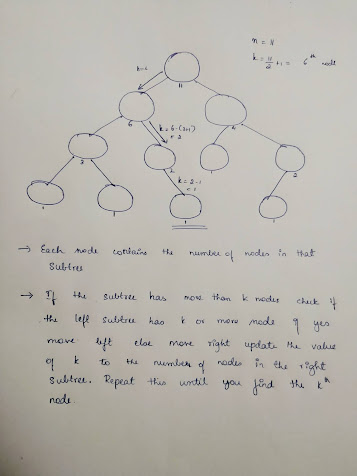
Solution 3: Using AVL Trees(or any height balanced BST) - O(logn), O(logn) time, O(1) space
The given problem can also be solved using AVL trees. Though the problem cannot be directly solved using AVL tree, it can be solved by making some adaptations to the AVL tree.
If we can store the nodes in the subtree for a given node ,then this information can be used to find the median. The root node will have the information of total number of nodes in the tree. If the total number of nodes 'n' is odd then median will be the ((n+1)/2)th node else the median will be the average of (n/2)th and (n/2 +1)th node. If the position of the median is less than the size of left subtree we move left , if the position is just one greater than the size of left subtree, then current node will be the median, else subtract the number of nodes in the left subtree +1(root node) from the median position and move to the right . Traverse tree until you find the node and return the median.
Complexity analysis:
Insert in balanced BST takes logirithmic time in worst case and so does addNum() which is a improvement from previous solution. findMedian() will also take logirithmic time as in worst case we have travel from root to the leaf of the tree which is a deterioration from previous solution. We still do not use any extra space.
Solution 4: Using two BST - O(logn), O(1) time, O(1) space
For the next two solutions we look at the problem from a different perspective. We aim at getting a O(1) complexity for finding the median. Hence instead of using one container that stores all the elements from the given stream, we can use 2 containers which partitions the given stream of elements into 2 partitions. The partitions should be such that given a stream of n-intergers:
CASE 1: If n is odd, container 1 should contain a[0], a[1], ... , a[k] and container 2 should contain a[k+1], a[k+2], ..., a[n-1] where a[0] < a[1] < ... a[k] and a[k+1] < a[k+2]< ... <a[n-1].
CASE 2: If n is even, container 1 should contain a[0], a[1], ..., a[k-1] and container 2 should contain a[k], a[k+1], ..., a[n-1] where a[0] < a[1] < ... a[k-1] and a[k] < a[k+1]< ... <a[n-1].
In CASE 1: We will have unequal sized containers. If we ensure that the difference of sizes of containers is not more than 1 if n is odd, then we get k = (n-1)/2 and the partitions become a[0], a[1], ..., a[(n-1)/2] and a[(n+1)/2], ..., a[n-1]. This means that a[(n-1)/2] will be the median of the entire stream and we can get this as maximum element of container 1.
In CASE 2: We need to ensure that we have equal size containers, and that means the partitions become a[0], a[1], ..., a[(n/2) - 1] and a[n/2], ..., a[n-1]. This means the mean of
a[(n/2) - 1] and a[n/2] will be the median of the entire stream and we can get these numbers as maximum element of container 1 and minimum of container 2 respectively.
Now we need to choose the right containers, which enables us to find median using the above discussions in constant time. If we think about it, at the end of the day we do not need such a container where we have the implicit ordering of a[0] < a[1] < ... a[k] , a[k+1] < a[k+2]< ... <a[n-1] and a[0] < a[1] < ... a[k-1] , a[k] < a[k+1]< ... <a[n-1]. But what we need is such a container where we can find max and min of the container in O(1) time and it rearranges itself such that we get max and min in O(1) time at all times in the future.
One such choice of a container can be a BST, as we can find max of BST on the rightmost leaf of the tree and min of the BST on the leftmost leaf of the tree. Fortunately for us balanced BST implementation of C++ STL's set/multiset keeps track of them on new insertion or deletion and hence accessible in constant time. We can use begin() and rbegin() to get leftmost and rightmost leaf of the tree respectively.
While inserting an interger, say num,
1. If both the containers have equal size(also both having size = 0 case), then insert an element num into container 1 if num <= max of container 1. If that is not the case, insert it into container 2.
2. If size of container 1 is less than size of container 2, then from our discussion we should at any point of time have difference in sizes not more than 1. Therefore, to ensure that size of container 2 doesn't go out of hand when an integer num such that num > min of container 2 is to be inserted, we perform the following 3 operations:
i. We store the min of container 2 in a temp variable and delete it from the container
ii. Insert temp into container 1
iii. Insert the new integer to be inserted, say num into container 2
3. Same goes for the condition when size of container 1 is greater than size of container 2. Analogous to the previous point, we do the following:
i. We store the max of container1 in a temp variable and delete it from the container
ii. Insert temp into container 2
iii. Insert the new integer to be inserted, say num into container 1
Finding the median is as simple as returning the mean of max of container 1 and min of container 2 if total number of intergers is even. If the total number of integers is odd and containers have unequal number of integers in them, then return max of container 1 if container 1 has one more integer than container 2 or return min of container 2 if container 2 has one more integer than container 1.
multiset<int> avl1; multiset<int> avl2; MedianFinder() { } void addNum(int num) { if(avl1.size()==avl2.size()){ if(avl1.size()==0 || num <= *avl1.rbegin()){ avl1.insert(num); }else{ avl2.insert(num); } }else if(avl1.size() < avl2.size()){ if(num <= *avl2.begin()){ avl1.insert(num); }else { int temp = *avl2.begin(); avl2.erase(avl2.begin()); avl1.insert(temp); avl2.insert(num); } }else { if(num >= *avl1.rbegin()){ avl2.insert(num); }else { int temp = *avl1.rbegin(); avl1.erase(avl1.find(temp)); avl2.insert(temp); avl1.insert(num); } } } double findMedian() { if(avl1.size()==avl2.size()){ return (*avl1.rbegin() + *avl2.begin())/2.0; }else if(avl1.size() < avl2.size()){ return *avl2.begin(); }else return *avl1.rbegin(); }
Complexity analysis:
Worst case in addNum() is when we do a sequence of operations erase(), insert(), insert() when size of containers are unequal. In a balanced BST each of insert and erase take logirithmic time and hence total time is O(3*log(n)) = O(logn).
As discussed above, we achieved O(1) time complexity for findMedian() by using this method as STL keeps track of max and min of the set/multiset in begin() and rbegin() respectively and hence are accessible in contant time.
We do not use any extra space other than the containers to store the stream of integers.
Solution 5: Using two Heaps - O(logn), O(1) time, O(1) space
Another choice of container for the discussion in solution 4 is a heap as we can find max of the container as the root of max heap and min of the container as the root of min heap and both in contant time. Insertion, Deletion is also no more that O(logn) and hence using heap also gives us an analogous solution as solution 4. Everything discussed in solution 4 including the algorithm remains the same while discussing the solution with 2 heaps. But we need to use a max heap as container 1 and min heap as container 2.
priority_queue<int> maxHeap; priority_queue<int,vector<int>,greater<int>> minHeap; MedianFinder() { } void addNum(int num) { if(maxHeap.size()==minHeap.size()){ if(minHeap.empty())minHeap.push(num); else if(num <= minHeap.top())maxHeap.push(num); else minHeap.push(num); }else if(maxHeap.size() < minHeap.size()){ if(num <= minHeap.top())maxHeap.push(num); else{ int temp=minHeap.top(); minHeap.pop(); maxHeap.push(temp); minHeap.push(num); } }else{ if(num >= maxHeap.top())minHeap.push(num); else{ int temp=maxHeap.top(); maxHeap.pop(); minHeap.push(temp); maxHeap.push(num); } } } double findMedian() { if(maxHeap.size()==minHeap.size()){ return (maxHeap.top()+minHeap.top())/2.0; }else if(maxHeap.size() > minHeap.size()) return maxHeap.top(); return minHeap.top(); }
Comments
Post a Comment